Updated: April 17, 2024
We searched for more codes!
Recommended Videos
King Legacy is an exciting Roblox game inspired by One Piece. You can choose between becoming a Marine or a Pirate and sail the seas to explore the vast world while upgrading your rank. There are also King Legacy codes you can redeem to get gold, resets, and much more!
All King Legacy Codes List
Active King Legacy Codes
- FREESTATSRESET: Use for a Stat Reset (New)
- UPDATE6: Use for 10 Copper Keys (New)
- DOUGHAWAKENING: Use for 20 Minutes x2Exp (New)
- ExperienceDoubling: Use for x2 Exp for 30 minutes
- 10KYZX-4LPQ8-WFJ: Use for a Stat Reset
- YT10K: Use for x2 Exp for 30 minutes
- shutdownhotfix: Use for x2 Gold Keys
- Peodiz10k: Use for x10 Gems
- Sub2Leepungg: Use for a 30-min free 2x Exp and 10 Gems
- 2MFAV: Use for a Stat Reset
- Peodiz: Use for x100k Cash
Expired King Legacy Codes
- Thx4Waiting
- UPDATE5
- UPDATE5SILVERKEY
- Halloween2023
- Update4.7
- HYDRAGLYPHICS
- UPDATE4.0.2
- UPDATE4.5.0
- UPDATE4.5.2
- lagshallnotpass
- 650KLIKES
- UPDATE3.5
- Update3_17
- 550KLIKES
- Update
- 500KLIKES
- 300KLIKES
- 400KLIKES
- 900KFAV
- 800KFAV
- 700KFAV
- 600KFAV
- Update2_17
- BeckyStyle
- 300MVISITS
- 500KFAV
- 250KLIKES
- GasGas
- KingPieceComeBack
Related: Z Piece Codes
How to Redeem Codes in King Legacy
To redeem codes in King Legacy, follow the step-by-step guide below:
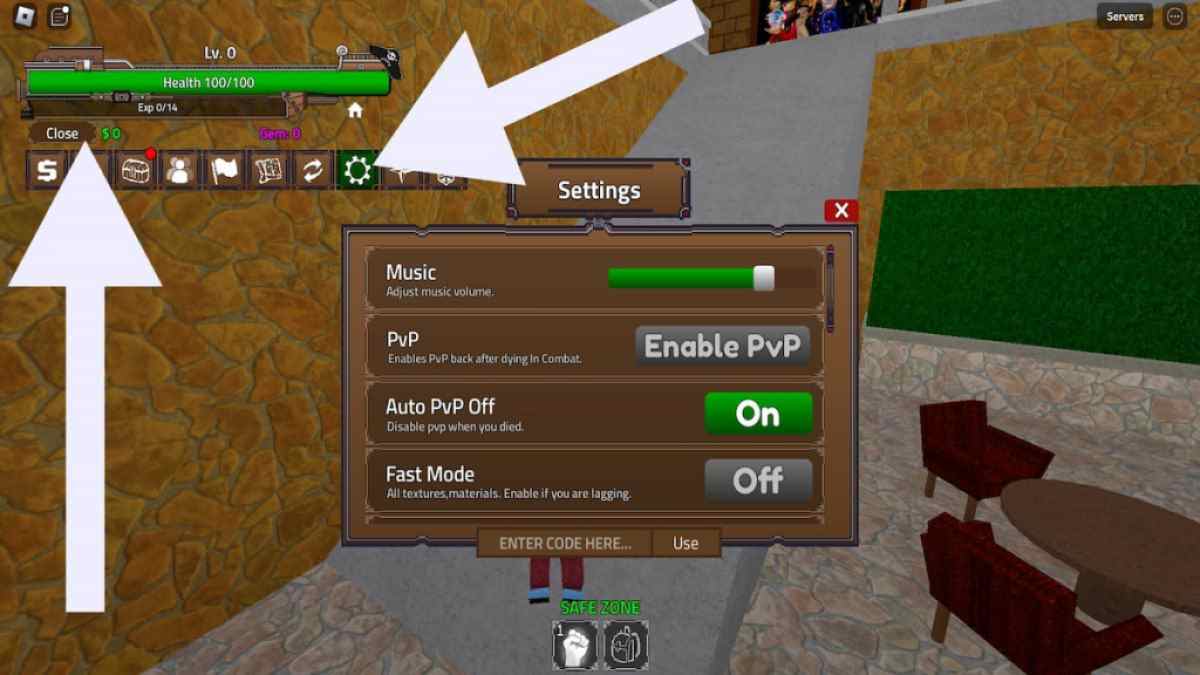
- Open King Legacy in Roblox.
- Click the Menu icon in the top-left corner of the screen.
- Click the cogwheel icon to go into Settings.
- Type the code into the text box at the bottom of the new window.
- Click Use and receive your freebies!
If you want to play more exciting Roblox games, check out our All Fruit Battlegrounds Codes in Roblox and All Grand Kaizen Codes articles to unlock other amazing goodies!
The Escapist is supported by our audience. When you purchase through links on our site, we may earn a small affiliate commission. Learn more





