Updated: May 10, 2024
We searched for the latest codes!
Blox Fruits is one of the most popular games around right now, and the One Piece-like title features codes just like many other Roblox titles, so in this article, we’re breaking down all the free goodies you can get now.
| JUMP TO: |
| Blox Fruits Codes in Roblox (February 2024) |
| How to Redeem Codes in Blox Fruits |
| How Codes Work in Blox Fruits |
| Where & How Can I Get More Blox Fruits Codes? |
| Why Aren’t These Codes Working? |
Blox Fruits Codes in Roblox
I’ve compiled a list below of all the active Roblox codes that you can use in Blox Fruits to get special, free rewards. I’ve checked all of these codes myself, so I can confirm that they were working as recently as this article’s last update. I’ve also tested it a few ways, and these codes aren’t case sensitive, so you don’t have to worry about that.
| Code | Reward |
| TRIPLEABUSE | 20 minutes of 2x Experience (New) |
| SEATROLLING | 20 minutes of 2x Experience (New) |
| 24NOADMIN | 20 minutes of 2x Experience (New) |
| NewtRoll | 20 minutes of 2x Experience |
| Kitt_Reset | Stat Reset |
| Chandler | $0 |
| Bluxxy | 20 minutes of 2x Experience |
| KittGaming | 20 minutes of 2x Experience |
| Enyu_is_Pro | 20 minutes of 2x Experience |
|
| |
| MagicBus | 20 minutes of 2x Experience |
| JCWK | 20 minutes of 2x Experience |
| StarcodeHEO | 20 minutes of 2x Experience |
| Sub2Fer999 | 20 minutes of 2x Experience |
| Sub2CaptainMaui | 20 minutes of 2x Experience |
| Sub2GamerRobot_EXP1 | 30 minutes of 2x Experience |
| Sub2GamerRobot_RESET1 | Stat Reset |
| Sub2NoobMaster123 | 20 minutes of 2x Experience |
| Sub2UncleKizaru | Stat Reset |
| Sub2Daigrock | 20 minutes of 2x Experience |
|
| |
| Sub2OfficialNoobie | 20 minutes of 2x Experience |
| Bluxxy | 20 minutes of 2x Experience |
| Axiore | 20 minutes of 2x Experience |
| TantaiGaming | 20 minutes of 2x Experience |
| StrawHatMaine | 20 minutes of 2x Experience |
| Fudd10 | $1 |
| Fudd10_V2 | $2 |
| BigNews | In-Game Title: “BIGNEWS” |
| TheGreatAce | 20 minutes of 2x Experience |
How to Redeem Codes in Blox Fruits
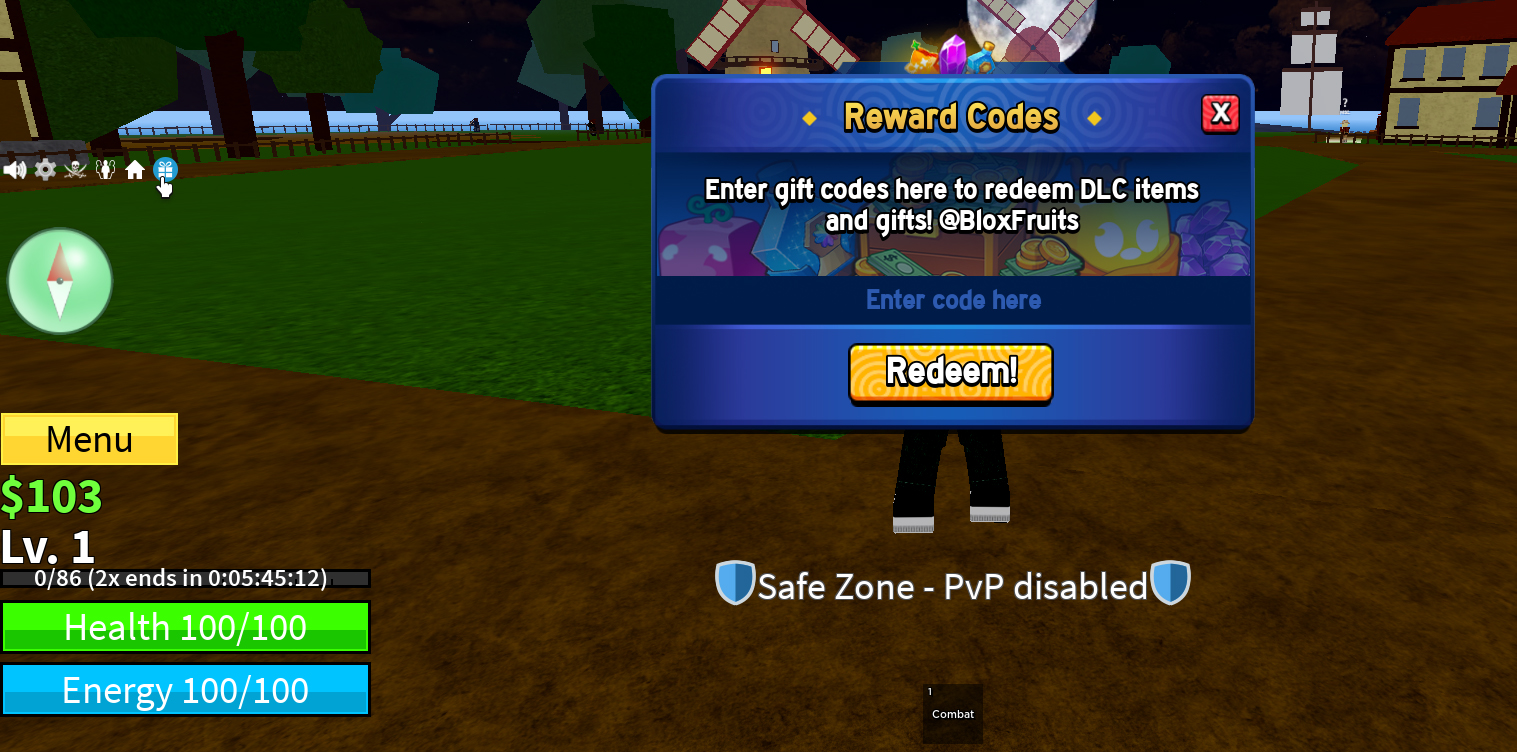
Redeeming codes in Blox Fruits is easy, and you can do it pretty much immediately after booting the Roblox game up. On the left-side of your screen, you’ll see a gift icon. Some sources call it a Twitter icon, but that information is out-of-date and is not accurate to current versions of Roblox.
Once you click on that icon, a “Reward Codes” window will pop up. Enter your code in the appropriate box and push “Redeem!” That should get you the promised reward. If it doesn’t, I’ll cover some steps to troubleshoot the problem later in the article.
How Codes Work in Blox Fruits
Codes in Blox Fruits can get you a lot of different things, including but not limited to, stat resets, titles, money, or even bonuses to experience. Due to the nature of the codes, it’s a good idea to make sure you’re using them in moderation. Resetting your stats multiple times in a row won’t do anything except exhaust your codes.
New codes are released regularly, often in celebration of a holiday, a new update, or some other milestone. As such, you should make sure to keep an eye on this list, as you never know when a new code is going to drop, and you really don’t want to miss out on these goodies!
Where & How Can I Get More Blox Fruits Codes?
There are a ton of different ways to get codes for the game. I always recommend checking out various social medias for Blox Fruits and other Roblox games. You can find the game on X at this link, and on Discord here. As always, stay safe and don’t pay anyone for codes.
Why Aren’t These Codes Working?
There are a few reasons one of the above codes might not be working. The most obvious culprit is that you’ve already entered the code before. All of them are single use, and so you won’t be able to use them a second time. It’s also possible that you might not be able to access the reward yet. There are some, such as codes for titles, that can only be accessed once you’ve gotten far enough in the game, even though you can redeem the code before that point.
Additionally, it’s possible the code as expired and we just haven’t updated the above list yet. Although we strive to keep this as up-to-date as possible, everyone here at The Escapist does their best to sleep at least occasionally, which means we might just not be around to do it. I swear, we’ll get to it as soon as possible.
And those are all the codes for Blox Fruits, which is part of Roblox. We’ll be updating this list and removing things as they expire.
Blox Fruits is available to play in Roblox now.





